Deep Learning Basic 10 - RNN
in AI Tech on ⁃ AI Basic

Intro
시퀀스 데이터의 개념과 특징, 그리고 이를 처리하기 위한RNN- RNN에서의 역전파 방법인
BPTT와기울기 소실문제에 대해 학습- 시퀀스 데이터만이 가지는 특징과 종류, 다루는 방법, 그리고 이를 위한 RNN(Recurrent Neural Network)의 구조를 CNN이나 다른
MLP(Multi Layer Perceptron)와비교하면서 공부할 것- RNN에서의 역전파 방법인
BPTT(Back Propagation Through Time)를수식적으로 이해하고, 여기서기울기 소실문제가 왜 발생할 수 있는지, 이에 대한해결책은 어떤 것들이 있는지를 집중
1.시퀀스 데이터

시퀀스 데이터: 순차적으로 들어오는 데이터를 의미하며 소리, 문자열, 주가 등의 데이터들을 시퀀스 데이터로 분류
- 문자열의 경우 문자를 인위적으로 나열하는 것이 아니라 문법, 문맥, 단어의 사용, 문장을 쓸 때, 이러한 의도 이런 것들이 반영 돼서 텍스트들이 시퀀스로 데이터를 기록하게 됨
- 주가의 경우, 어떤 독립된 정보들이 주가에 반영되는 것이 아니라, 시간 순서대로 기업의 성장, 시장의 상황, 불규칙적 사건의 발생 등이 종합돼서 시점 별로 나타나는 시계열데이터의 특징으로, 시퀀스 데이터의 경우 이벤트의 발생순서가 중요한 요소 중 하나로 동작하게 됨

💡 시퀀스 데이터는
독립동등분포(i.i.d.)가정을 위반하기 쉽다.
- 예를 들어, ‘개가 사람을 물었다’와 ‘사람이 개를 물었다’라는 2개의 문장이 있다면, 전자는 비교적 많이 발생할 수 있지만 후자는 위치를 바꾸게 됨으로써 의미가 바뀌고 데이터에서 관측되는 빈도도 바뀌게 됨
- 이처럼 순서를 바꿨을 때, 데이터의 확률 분포가 바뀌거나 혹은 과거의 정보를 가지고 미래를 예측할 때, 만약 과거의 정보에 손실이 발생 해 미래정보 예측 시 과거 정보를 모두 쓸 수 없고,
한정된 정보만 사용할 수 있는 경우, 시퀀스 데이터는 예측분포의 성격이 달라질 수 있음- 따라서, 데이터의 순서를 바꾸는 등 인위적 조작을 통해 예측하면 미래예측이 어려워지기 때문에, 원하고자하는 모델링이 잘 되지 않을 확률이 높아지게 됨
- 시퀀스 데이터는 쉽게 독립동등분포가 깨질 수 있기 때문에
위치를 바꿀 때 조심해야 함- 이런 특성을 반영해서, 학습을 진행할 때 순차적으로 들어오는 정보를 어떻게 반영할지 고민해야 함

- 과거의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다룰 때
조건부확률이용 가능
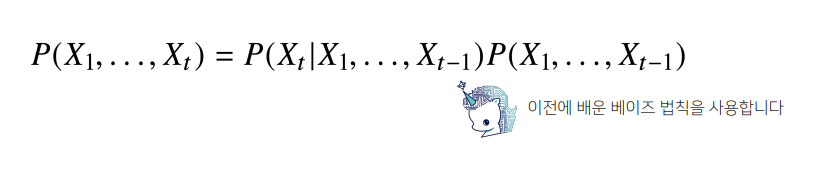
- 결합확률분포 $P(X_1,…,X_t)$를 베이즈법칙을 통해 조건부확률을 쪼갤 수 있음
- $X_1,…,X_{t-1}$의 정보가 주어졌을 때 $X_t$에 대한 조건부확률분포에 $P(X_1,…,X_{t-1})$까지의 결합확률을 곱해주면, $P(X_1,…,X_t)$ 결합확률분포를 모델링할 수 있음

- 이처럼 조건부확률을 분해하는 것을 반복적으로 적용하면, 맨 하단 수식처럼 $X_{s-1},…,X_1$까지의 조건부를 가지고, $X_s$를 추론하는 조건부확률을 $X_1,…,X_t$까지 쭉 곱해주는 형태로 표현 가능
- $\prod$ (파이) : s = 1, … ,t까지 기호를 쓴 것이 모두 곱하라는 기호
- 조건부확률을 곱셈으로 전개하기 때문에, 결합확률분포를 조건부확률을 이용해 모델링하는 것이 가능하고, 맨 초기 시점 $X_1$부터 바로 직전의 과거정보인 $X_{s-1}$시점까지의 정보를 사용해 현재시점인 $X_s$를 모델링하는 조건부확률분포를 반복적으로 곱해주는 형태로 모델링 할 때 사용

💡 $X_t$를 모델링 하는 조건부확률분포의 모델링이 시퀀스 데이터를 다루는 기본적인 방법론
- 다만, 위 조건부 확률을 다룰 때 과거의 모든 정보를 사용하는 것처럼 기재했지만, 사실 시퀀스데이터를 분석할 때 모든 과거의 정보들이 필요한 것은 아니다.
- 어떤 기업의 주가를 갖고 모델링 할 때, 기업이 20~30년 된 오래된 기업이고 2021년 주가를 예측한다고 하면, 기업의 창립부터 30년치 데이터가 필요한 것이 아니다.
- 이 때, 5년정도 지속한 사업정보를 통해 예측하는 것과 같이 최근의 정보들을 주로 다루는 것이 적절하기 때문에 과거의 모든 정보를 항상 필요한 건 아니다.
- 일부, 데이터 분석 결과에서 일부 과거 정보들을 truncation 하는 것을 테크닉으로 이용할 수 있기 때문에, 조건부확률 모델링에서 과거의 모든 정보를 활용할 필요는 없으며 이는 텍스트, 음성도 동일함
- 어떤 문장을 생성한다 했을 때, 앞 뒤 맥락을 보고 파악해서 문장을 생성하거나 문법을 파악하는 것이 중요하고 1page부터 볼 필요는 없음
- 따라서, 시퀀스 데이터를 다룰 때 과거의 어떤 시점에서의 정보는 필요하지 않을 때가 있기 때문에, 필요성에 따라 과거의 정보를 어떻게 활용할지 모델링의 방법에 따라 바뀔 수 있는 사실을 기억해야 함

- 이런 조건부확률분포를 반복적으로 사용해서 미래 예측에 대한 분포로 모델링할 수 있음
- 문제는 시퀀스 데이터를 다루기 위해, 길이가
가변적인 데이터를 다룰 수 있는 모델이 필요- $X_t$의 경우 $X_1,…,X_{t-1}$까지 $t-1$개의 정보가 필요할 것이고, $t+1$의 경우 $X_1,…,X_t$까지 t개의 정보가 필요한 모델이 필요
- 이처럼 시퀀스 시점에서 다뤄야 할 데이터의 길이가 달라지기 때문에, 조건부 모델로 시퀀스 데이터를 다룰 때는 가변적인 길이의 데이터를 다룰 수 있는 모델과 방법론이 필요

- 과거의 모든 정보를 가지고 예측을 할 필요는 없음
- 만약, 현시점에서 최근 몇 년 간 데이터 혹은 몇 개의 문장만 보고 충분히 모델링 가능한 경우, 초기시점부터 모든 정보를 사용할 필요 없이
고정된 길이 τ(tau)만큼 시퀀스만 사용해서 예측 가능- 이 경우 가변적 길이가 아닌,
τ라는 고정된 길이를 사용하는 모델이 됨- $X_t$의 분포를 계산할 때 $t$ ~ $t-τ$까지
τ개의 정보를 활용 가능- $t+1$시점의 미래예측을 위해 $t$ ~ $t-τ+1$까지
τ개의 정보를 활용 가능- 즉 고정된 길이를 가지고 예측할 때 Autoregressive 모델 중에서도 τ인 경우 해당하기 때문에, 이런 형태의 모델링을 통해서도 시퀀스 데이터를 다룰 수 있음
- 문제는 τ는 Hyper parameter 모델링 하기 전 사전에 정해줘야하는 변수가 되기 때문에, τ를 결정하는 것은 사전지식이 필요할 때가 있으며 문제에 따라 τ가 바뀔 수도 있음
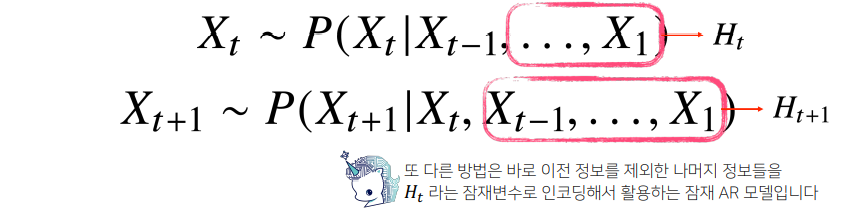
💡 이런 경우 모델링은 어떡해야 할까?
- 이 경우, RNN의 기본 모형인 잠재 자기회귀 모델을 통해 직전 정보와 훨씬 과거의 정보를 묶어서 직전 정보와 직전 정보가 아닌 과거의 정보들을 따로 모음
- $X_{t-1}$ : 이전 직전 정보
- $X_{t-1}$ 이전의 정보 : $X_t-H_t$(잠재변수)로 인코딩
- $X_t$를 예측할 때 $X_1$~$X_{t-2}$까지의 정보를 가지고 $H_t$라는 잠재변수를 만듦
- $X_{t+1}$에서는 $X_1$~$X_{t-1}$정보를 갖고 $H_{t+1}$라는 잠재변수를 만듦
- 이 경우, 바로
직전의 정보와잠재변수이 2개의 데이터를 갖고 미래시점을 예측할 수 있기에, 가변적이지 않은고정된 길이의 데이터를 가지고 모델링 할 수 있게 됨- 이 모델의 장점은 과거의
모든 데이터를 활용해 예측할 수 있고, 가변적 데이터의 문제를고정된 길이의 문제로 바꿀 수 있기 때문에 여러 장점을 갖고 있는 모델이라고 할 수 있음
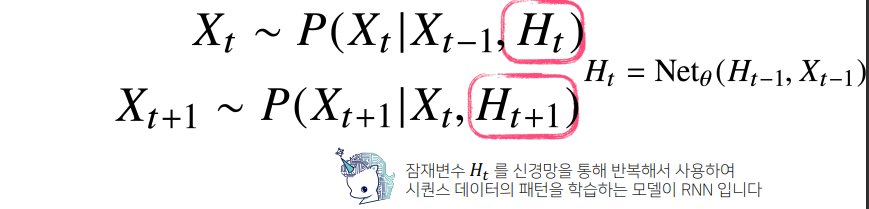
💡 과거의 정보들을 잠재변수로 어떻게 인코딩할지에 대한 선택의 문제
- 이를 위해 등장한 것이 RNN이며, 이는 $H_t$를 NN을 통해 바로 이전의 정보와 이전 점재변수의 모형을 갖고 예측해 시퀀스 데이터의 패턴을 학습하는 모델
2. Recurrent Neural Network

- RNN은 MLP와 유사한 모양
- 입력행렬 x로부터 가중치행렬 W를 곱해주고 b를 더해준 후, 활성화함수를 합성해서 잠재변수 H를 만들어주고 H에 다시 선형모델을 결합시켜 출력행렬인 O가 되는데, W1과 W2는 각각 첫 번째 레이어의 가중치 행렬, 두번째 레이어의 가중치 행렬이 됨
- 이때 W1과 W2는 시퀀스 데이터와 첫번째 시점의 데이터 또는 두번째 시점의 데이터 상관없이 share하는 가중치 행렬로 이해하면 됨

- MLP 모델은 시퀀스 데이터를 입력으로 모델링할 때, 과거의 정보를 다룰 수 없음
- 오로지 입력행렬이 t번째만 들어와 현재 시점을 갖고 예측이 가능한 모델이기 때문에, MLP의 경우 과거의 정보와 잠재변수를 다룰 수 없음
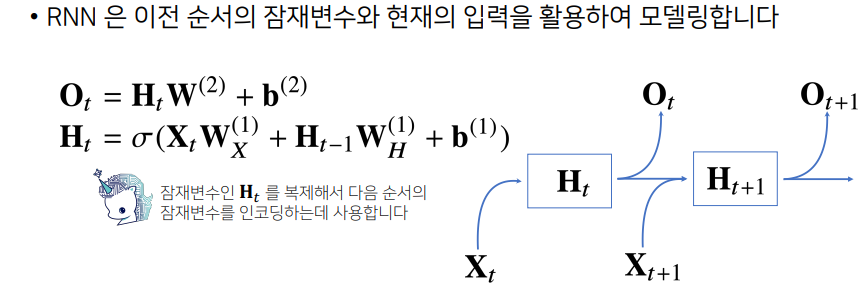
💡 어떻게하면 과거의 정보를 $H_t$안에 담을 수 있을까?
- RNN은 이전 순서와 잠재변수와 현재의 입력을 활용해 모델링
- 즉, 앞에서의 차이점은 $H_t$텀을 표현할 때, 중간의 새로운
가중치 행렬이 등장하게 됨
- $W_x$ 가중치행렬 :
입력으로 부터 전달됨- $W_h$ 가중치행렬 : 이전
잠재변수로 부터 전달됨- t번째 잠재변수는 현재 들어온 입력벡터의 $X_t$와 이전시점에 잠재변수인 $H_{t-1}$을 받아, 현재시점의 잠재변수인 $H_t$를 만들고, $H_t$를 이용해 현재시점의 출력인 $O_t$를 만들게 됨
- 이 때 잠재변수 $H_t$를 다음시점인 $H_{t+1}$에 다시 사용하게 됨으로써, $H_t$라는 잠재변수를 복제하고, $H_t$를 복제해서 다음순서 $H_{t+1}$에 인코딩하는데 사용하게 됨
- 유의해서 봐야하는 것은 가중치 행렬이 3개가 나오게 됨
- 먼저 첫번째 레이어에서는 $W_x^{(1)}$ 입력 데이터에서부터 선형모델을 통해 잠재변수로 인코딩하게 될 $W_x^{(1)}$과 이전 시점의 잠재변수로부터 정보를 받아서 현재 시점의 잠재변수로 인코딩 해주는 $W_h^{(1)}$ 즉 첫번째 레이어에 가중치행렬 $W_h$를 사용하게 되는 것
- 이렇게 만든 잠재변수를 통해 다시 출력으로 만들어주는 $W2$ 가중치행렬이 존재해서 총 3개의 가중치 행렬이 있게 됨
- 명심해야하는 것은 $W2$, $W_x^{(1)}$, $W_h^{(1)}$ 이렇게 3개의 가중치 행렬은
t에 따라 변하지 않는 가중치행렬이라는 사실을 기억해야함- 즉, t에 따라 변하는 것은 오로지
잠재변수와입력 데이터에 해당하는 것이고, RNN에서 사용되는 $W_x$, $W_h$, $W_o$, $W2$에 해당하는 가중치 행렬들은 t에 따라 변하지 않는 행렬이라는 사실을 기억해야 함- 이 가중치 행렬들은 동일하게 각각
t시점에서 활용되어 모델링을 하게 됨
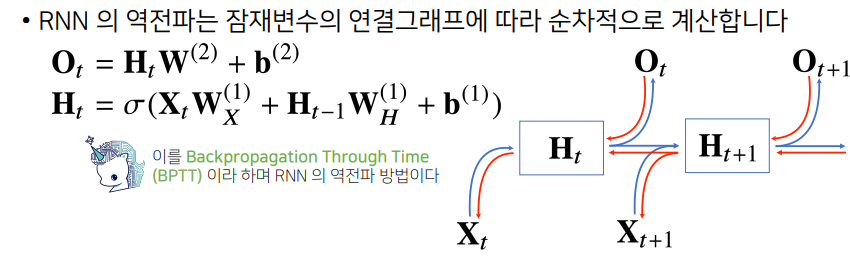
- 위 방법론들은
순전파에 해당하는 계산 방법이며,역전파는 거꾸로 gradient가 흐르는 것- 역전파는 잠재변수들의 연결 그래프에 따라 순차적으로 계산하게 되는데, $X_1$~$X_t$시작해서 RNN의 모든 시점에서의 예측이 전부 이뤄진 다음,
맨 마지막 시점에서 gradient가 점점 타고 올라와서과거까지흐름- 이는
BPTT라는 RNN의 역전파 방법이며, 그림처럼 빨간색 선으로 이뤄진 것이 gradient의 전달 경로잠재변수에 들어오는gradient는 2개가 들어오게 됨- 바로
다음 시점에서의 잠재변수에서 들어오는 gradient 벡터와출력에서 들어오는 gradient 벡터와 같이 2개가 잠재변수에 전달이 되고, 이 잠재변수에 들어오는 gradient 벡터를입력과그 이전시점의 잠재변수로 전달하고 이를반복해서RNN의 학습이 이뤄짐
3. BPTT

- 모든 t 시점에서의 loss function를 계산한 다음에 gradient를 계산하는 형태
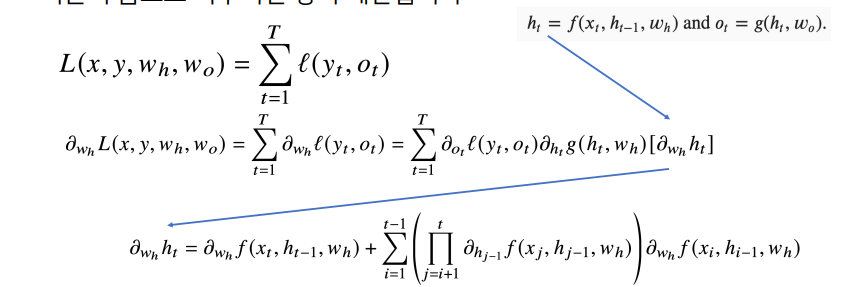
- 중요 과정만 설명하면
BPTT를 통해 각가중치행렬의 미분을 계산할 때

- 최종적으로 나오는 product 텀, 다시 말해 $i+1$ ~ $t$시점까지 모든 잠재변수에대한 미분 텀이 곱해지고 더해짐
- 이는
현재시점~ 예측이 끝나는t시점까지 시퀀스 길이가 길어질수록, 곱해지는 텀들이 불안정해지기 쉬움- 이 값이 1보다 크면 굉장히 커지고 1보다 작으면 굉장히 작은 값이 되기 때문에,미분값이 엄청 커지거나 작아지게 될 확률이 높음
- 따라서,
BPTT를 모든 시점에서 적용하게 되면RNN의 학습이 불안정되기 쉬움
4. 기울기 소실의 해결책?

- BPTT를 모든 t시점 (관찰되는 모든 예측 순간)에 적용하면, gradient를 전부 곱해주는 형태이기 때문에, gradient 계산이 불안정해질 확률이 높아짐
- 특히, gradient가 0으로 줄어드는 즉 Vanishing(소실)하는 것이 굉장히 큰 문제가 됨
- 그 이유는 미래시점에 가까울수록 gradient가 살아있고 과거로 갈수록 0으로 가게 되면, 과거 시점에 대해 앞선 이전 시점에서의 예측모델에 대한 반영이 쉽지 않기 때문에, 과거 정보를 무시하게 될 확률이 높게 됨
- 만약, 문맥적으로 이전 시점의 정보가 필요한 텍스트 분석이나 긴 시퀀스를 분석해야하는 문제들의 경우는 BPTT를 가지고 그라디언트를 계산해서 학습을 진행할 때 gradient가 0으로 줄기 때문에 과거의 정보를 잃어버리는 문제가 발생하기 쉬움
- 이 문제 해결을 위해,
truncated BPTT사용함 - BPTT의 모든 시점을 계산하는 것이 아니라 미래 정보들에서 몇 개는 gradient를 끊고, 오로지 과거의 정보에 해당하는 몇 개의 블록을 나눠서 이 BPTT를 연산하는 과정으로 위 그림과 같음
- 잠재변수에 들어오는 gradient를 쭉 받아올 때, 미래 시점부터 $t+1$시점까지 들어오는 gradient를 받다가, 여기서부터 들어오는 gradient를 $H_t$에 전달하지 않음
- $H_t$는 오직
출력에서 들어오는 gradient인 $O_t$에서만 받아 $H_t$에 전달 - 이처럼 gradient를 전달할 때, 모든 t시점에서 전달하지 않고 특정 블럭에서 끊어 gradient를 나눠서 전달하는 방식이
truncated BPTT - 이 방법을 통해 gradient vanishing을 해결 할 수 있지만, 완전한 해결책은 아님
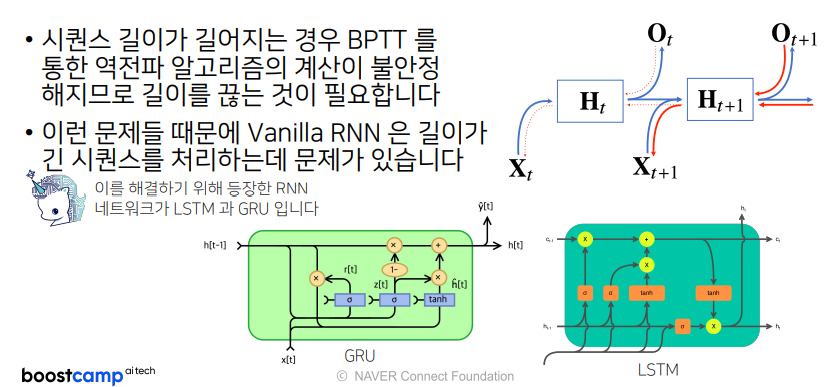
- 오늘 날에는 gradient vanishing 문제 때문에 기본적인 RNN 모형을 사용하지 않고,
- 길이가 긴 시퀀스를 처리하는데에는
LSTM,GRU라는 다른 advanced된 RNN을 사용
소통은 제가 공부하고 공유하는 원동력이 됩니다.
해당 글이 도움이 되셨다면 소중한 격려와 응원 부탁드립니다 ☺️
해당 글이 도움이 되셨다면 소중한 격려와 응원 부탁드립니다 ☺️
