Deep Learning Basic 05 - Gradient Descent Method
in AI Tech on ⁃ AI Basic

Intro
- 최적화와 관련된 다양한 Gradient Descent 기법
- 기존 SGD(Stochastic gradient descent)를 넘어서 최적화(학습)가 더 잘될 수 있도록 하는 다양한 기법
- Further reading
- Intro
- 1. 최적화와 관련된 다양한 Gradient Descent 기법
- 2. Gradient Descent Methods
- 3. Batch-size Matters
- 4. Gradient Descent Methods
- 5. Gradient Descent
- 6. Momentum
- 7. Nesterov Accelerated Gradient
- 8. Adagrad
- 9. Adadelta
- 10. RMSprop
- 11. Adam
1. 최적화와 관련된 다양한 Gradient Descent 기법
- 기존 SGD(Stochastic gradient descent)를 넘어 최적화(학습)가 더 잘 되는 다양한 기법
2. Gradient Descent Methods
- 10만 개 데이터가 있다고 가정하면 한 번에 1개만 봐서 Gradient를 구하고 이를 업데이트하는 걸 반복하며, 일반적인 딥러닝에서는 Mini-batch를 많이 활용
Stochastic gradient descent: 1개의 샘플로만 Gradient를 구해 업데이트Mini-batch gradient decent: 모두 사용하진 않거나 1개만 사용하는 것이 아닌, 샘플을 한 번에 활용해서 Gradient를 구해 업데이트Batch gradient decent: 한 번에 전부 사용해서 Gradient를 평균을 구하기 위해 업데이트

3. Batch-size Matters
적절히64~128개를 활용하는 것 좋음- large batch size를 활용하면 sharp minimizer에 도달하는 반면, small batch size는 flat minimizer에 도달
- 즉,
작게 쓰는 것이 실험적으로 좋다라는 것이 이 논문의 논점

- 목적 : test의
minimum을 찾고 싶음 - flat minimum의 특징은 training function에서 멀어져도
test function에서 적당히 낮은 값이 나옴- train data에서 잘 되면 test에서도 잘 된다는 의미
- sharp minimum은 test function에서 약간만 멀어져도 동작을 잘 안 함
- batch size를 줄이면 일반적으로 generation Performance가 좋아진다는 것을 실험적으로 보이고, large batch size 를 어떻게 활용하면 좋을지 테크닉적으로 말하는 논문

4. Gradient Descent Methods
- 자동으로 미분을 계산해주지만, optimizer를 직접 골라야 하므로 각각이 왜 발전했고 제한이 됐고, 성질이 있는지 알아두는 것이 좋음
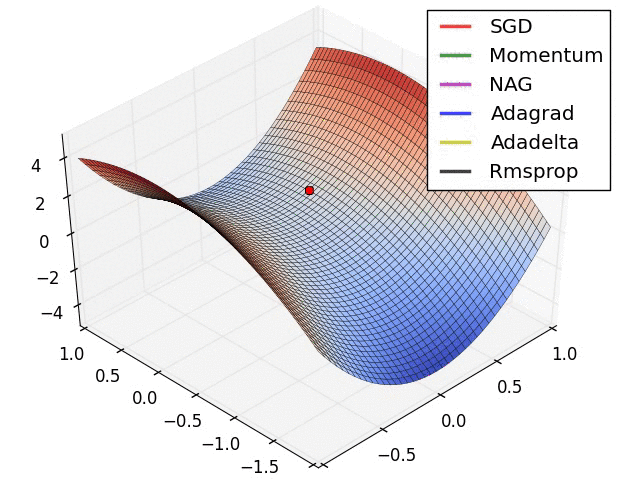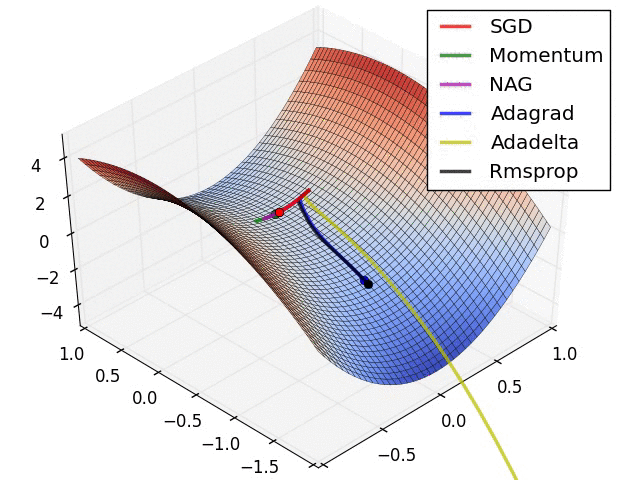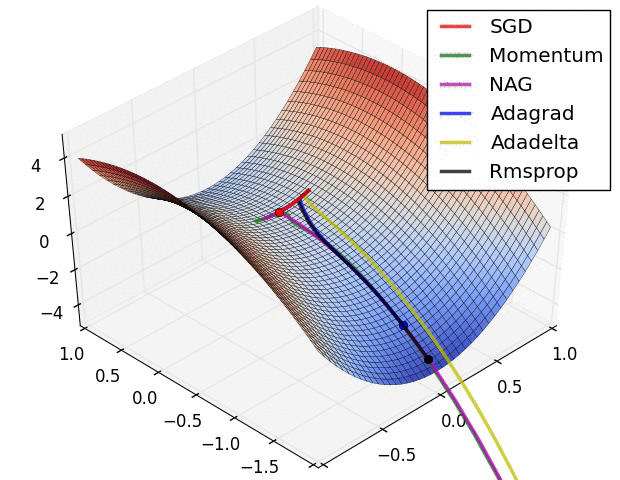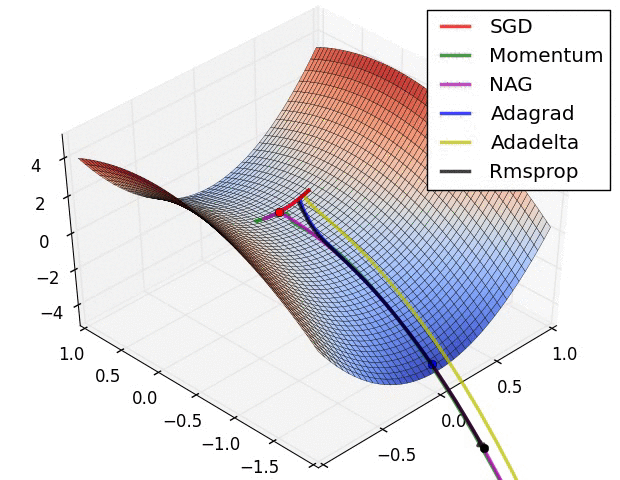
5. Gradient Descent
- \(W\) (weight, NN의 가중치)
- NN, 딥러닝의 framework가 기본적으로 해주는 것은 gradient를 계산 (=g)
- gradient descent를 기본적으로 활용하게 되면 gradient에 η(=eta)라고 불리는 step size만큼(learning rate) 곱해서, \(W_t\)에서 빼주면 업데이트 됨 → gradient descent (\(W_{t+1} =W_t-ηg_t\))
- 문제점은 learning rate 혹은 step size를 잡는 것이 매우 어려움, 크면 잘 안 되고 작으면 학습을 아무리 시켜도 안 됨, 따라서 적절히 잡아주는 것이 매우 중요

6. Momentum
- 이런 것을 발전시키고자 혹은 똑같이 gradient 정보만 활용해도 더 좋은 성능을 내고 더 빨리 학습을 시키기 위한 optimization 테크닉들이 나오게 되고 이 중 가장 기본이 되는 것 momentum
- 결국 한 번
gradient가 a방향으로 갔을 때,b방향으로 가도a방향으로 갔던 정보를 이어가기 위함- 이를 사용하는 이유는 mini batch를 사용하기 때문에, 다음 번 batch static로는 a방향으로 흐르게 돼도, a정보를 최대한 활용하기 위함
- 이를 사용하는 이유는 mini batch를 사용하기 때문에, 다음 번 batch static로는 a방향으로 흐르게 돼도, a정보를 최대한 활용하기 위함
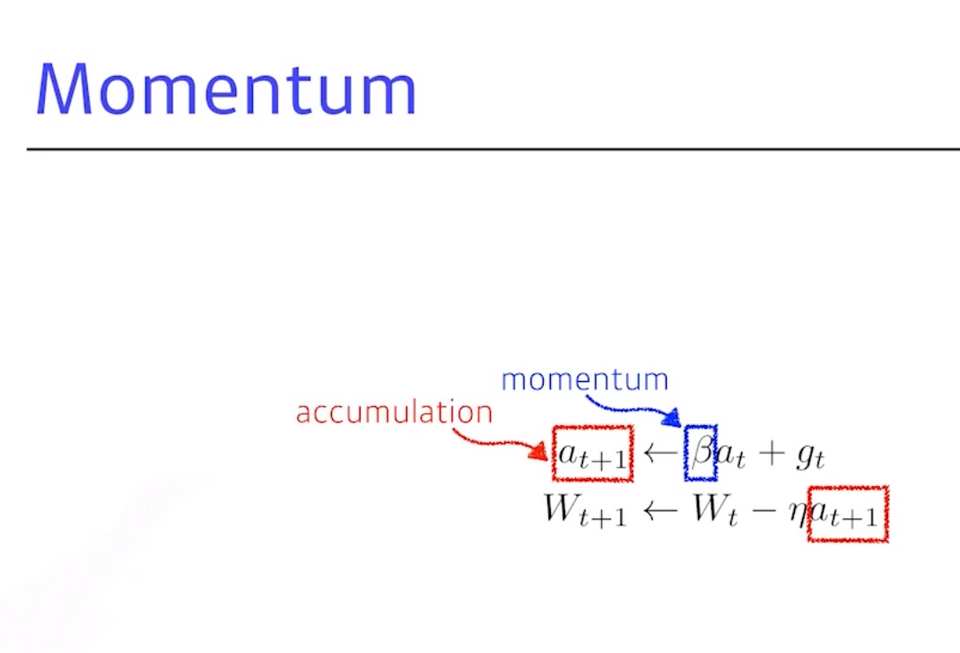
- Beta(=Hyper parameter)가 들어가 이것이 momentum을 잡게 되고, g(=gradient)가 들어오면 다음(t+1째)에 이 g를 버리고 gt+1을 사용하는 것이 아니라,
a(=momentum)텀이 그 값을계속 들고 있는 것 - 그래서 momentum과 현재 gradient를 합친
accumulation(축적)으로, momentum이 포함된 gradient로 업데이트 됨 - 이 장점은 한번 흐른 gradient direction을 어느 정도 유지시키기 때문에, gradient가 굉장히 많이 왔다갔다해도 잘 학습시킬 수 있음
\(a_{t+1} = Ba_t +g_t\) → a = accumulation / B(Beta) = momentum \(W_{t+1} =W_t-ηg_{t+1}\)
7. Nesterov Accelerated Gradient
- 조금 비슷하지만 약간 컨셉이 다름
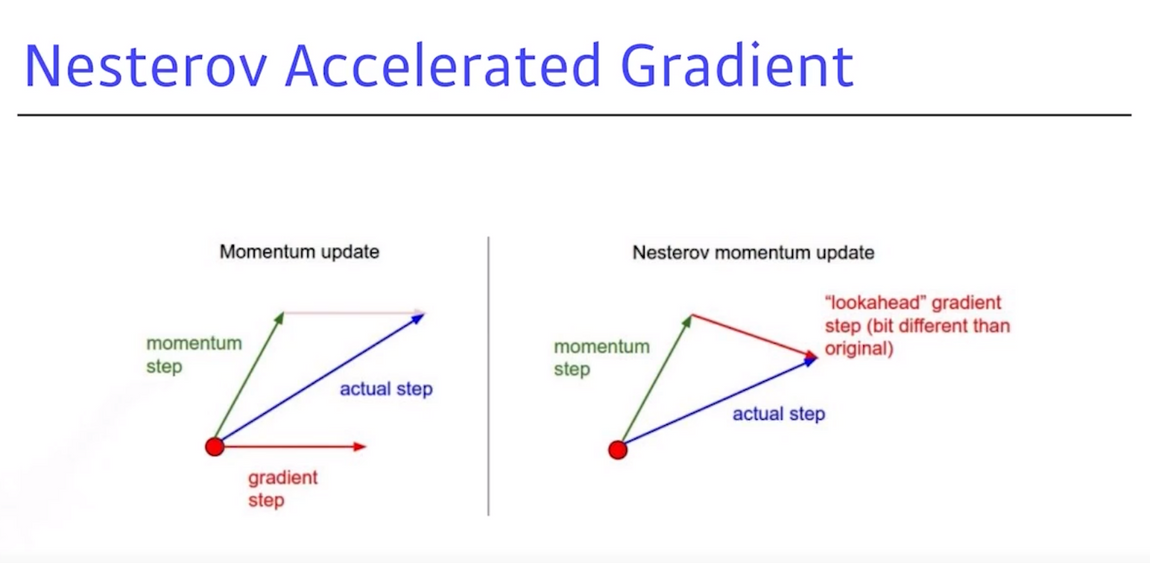
NAG: a라는 gradient가 결국 gradient decent를 하는 것인데, gradient를 계산할 때 lookahead gradient를 계산- 원래 momentum은 현재 주어진 파라미터에서 gradient를 계산해서 그 gradient를 가지고 momentum을 accumulation을 했다면,
NAG는 한 번 이동을 함- 즉, a라고 불리는 정보가 있으면
한 번 가 보고,간 방향에서 gradient를 계산한 것을 가지고 accumulation을 하는 것
- 즉, a라고 불리는 정보가 있으면

Momentum update: local minimal에서 a라는 슬로프(기울기)가 있으면 a로 가게 되므로, local minimum을 지나 슬로프의 반대편으로 가게 되고, a방향에서의 Momentum이기 때문에 a로 흘러도 올라가는 현상이 발생- 이 때, 올라갔다 내려갔다를 반복하게 되는데 일반적으로 모멘텀을 관성으로 봤을 때, local minimal으로 들어가지만 계속 converting하게 돼서 local minimal를 converting을 못하는 현상이 발생
NAG: 이에 반해 a방향으로 gradient가 생기면local minimal을 지나간 그 자리에서 계산하기 때문에 local minimal이아래로 가는 현상이 발생- 이 때 장점은 local minimal을 봉우리의 가장 끝 점으로 볼 수 있는데, 이 봉우리에
빨리 converting 가능
- 이 때 장점은 local minimal을 봉우리의 가장 끝 점으로 볼 수 있는데, 이 봉우리에
8. Adagrad
- 이때부터는 NN의 파라미터가 얼마만큼 변화했는지 혹은 안 변했는지를 확인
- NN의 파라미터가
많이 변한 파라미터에 대해서는 더 적게변화시키고,안 변한 파라미터는 많이 변화시키고 싶음 - 지금까지 각 파라미터가 얼마만큼 변했는지의 값을 저장해야 하며, 이것은
G (Sum of gradient squares, 제곱해서 더한 것)가 됨 - G가 계속 커지면, 해당하는 파라미터가 많이 변했다는 것을 의미
- 이것을
역수에 집어넣기 때문에 지금까지많이 변한 파라미터는 적게변화시키고적게 변한 파라미터는 많이변화시킴 - 가장 큰 문제는
G가 계속 커지기 때문에, G가 무한대로 가게 되면 분모가 무한대가 되므로 W의 업데이트가 안 되고 뒤로 갈수록학습이 멈추 현상이 발생- 이러한 문제를 해결하기 위한 것 →
Adadelta
- 이러한 문제를 해결하기 위한 것 →

9. Adadelta
Adadelta: adagrad가 가지는 문제, 계속해서 커지는 현상을 막기 위한 방법론- 이론적으로 막을 수 있는 가장 쉬운 방법은 현재 t가 주어졌을 때 이를 어느 정도 Window size만큼 파라미터, 시간에 대한 gradient 제곱의 변화를 보겠다라고 하면 되는데, 문제는 Window size를 100개로 잡으면 이전 100개 동안의 g라는 정보를 들고 있어야 함
💡
Window size: 한 번에 받을 수 있는 데이터의 양으로, 통신을 할 때 상대방에게 자신의 Windows size를 알려주면, 상대방은 그만큼의 양을 한번에 전송을 하고 상대방이 다 처리했는지 확인 후에 다음 데이터를 전송하는 것- 이를 막을 수 있는 것이
EMA (Exponential Moving Average)→ 어떤 값이 있을 때감마를 곱해주고 더해주면, 어느 정도 time window만큼 값을 저장하고 있는 것의 평균 값, 그것에 대한 합을 갖고 있는 것으로 볼 수 있음- 이렇게 EMA를 통해 G를 업데이트하는것이 Adadelta
- \(g_t\)의 크기를 생각해보면 gradient는 모든 파라미터 하나만 들고 있기 때문에, 예를들어 gpt3 같은 1000억 개 파라미터가 들어있는 모델을 쓰면 \(g_t\)자체도 1000억 개 파라미터인 것. 즉, 엄청난 양의 파라미터를 들고있어야 하므로 모델이 터져버릴 수 있음
- 이렇게 바꾸고, H라는 다른 파라미터가 들어가는 것이 전부
Adadelta는 Adagrad에서 가지고 있던 learning rate가 G의 역수로 표현됨으로써 생기는monotonicall decreasing(단조로운 감소)을막는 방법으로 볼 수 있음- 반면, Adadelta의 가장 큰 특징은
learning rate가 없어 바꿀 수 있는 요소가 없기 때문에 사실 상 많이 활용되지 않음

10. RMSprop
- 해당 방법론은 논문이 아닌, Geoff Hinton이 딥러닝 강의를 하다가 본인이 해보니 하니 잘 돼서 제안
- Adagrid처럼 gradient scales에 대한 것을 그냥 더하는 것이 아닌,
EMA를 더해 분모에 넣고 대신η(eta)에 stepsize가 들어가 있음

11. Adam
Adam : Adaptive Moment Estimation (일반적으로 가장 잘 되고, 무난)
gradient scales를EMA를 가져감과 동시에momentum을 같이 활용하는 것- gradient 크기가 변함에 따라 혹은 scales 크기에 따라
adaptive learning해서 바꾸는 것과 이전에 gradient 정보에 해당하는moment를 잘 합친 것이 Adam - 이 둘을 잘 섞어서
Hyper parameter와Momentum을 얼마나 잘 유지시킬지, scales에 대한 EMA 정보 즉,η(=learning rate),Epsilon(=parameter)와 같이, 4개의 파라미터를 조정하는 것도 중요 - Adam은 여러 파라미터가 들어가고, 실제 Epsilon이 값을 잘 바꾸는 것이 매우 중요
- 구현할 필요는 없고, 파이토치 텐서플로우를 쓸 때 한 줄을 잘 바꾸면 될 것

소통은 제가 공부하고 공유하는 원동력이 됩니다.
해당 글이 도움이 되셨다면 소중한 격려와 응원 부탁드립니다 ☺️
해당 글이 도움이 되셨다면 소중한 격려와 응원 부탁드립니다 ☺️
