Deep Learning Basic 07 - CNN (Convolutional Neural Network)

in AI Tech on ⁃ AI Basic
Deep Learning Basic 07 - CNN (Convolutional Neural Network)

Intro

  • CNN(Convolutional Neural Network)에서 가장 중요한 연산은 Convolution으로, CNN에 대한 공부를 하기 전에 Convolution의 정의, convolution 연산 방법과 기능을 공부
  • 그리고 Convolution, 입력을 축소하는 Pooling layer, 모든 노드를 연결하여 최종적인 결과를 만드는 Fully connected layer 로 구성되는 기본적인 CNN(Convolutional Neural Network) 구조를 공부

1. Convolution (합성곱)

  • convolution은 2개의 함수 f, g가 있을 때 이 2개를 잘 섞어주는 Operator로 정의
  • convolution Operator를 Discrete convolution으로 쓰면 2번째 수식으로 볼 수 있음
  • 우리가 실제로 많은 알고있는 2D convolution은 3번째 수식으로 적을 수 있음
    • 여기에서 I는 전체 이미지의 공간, K는 적용하고자 하는 convolution

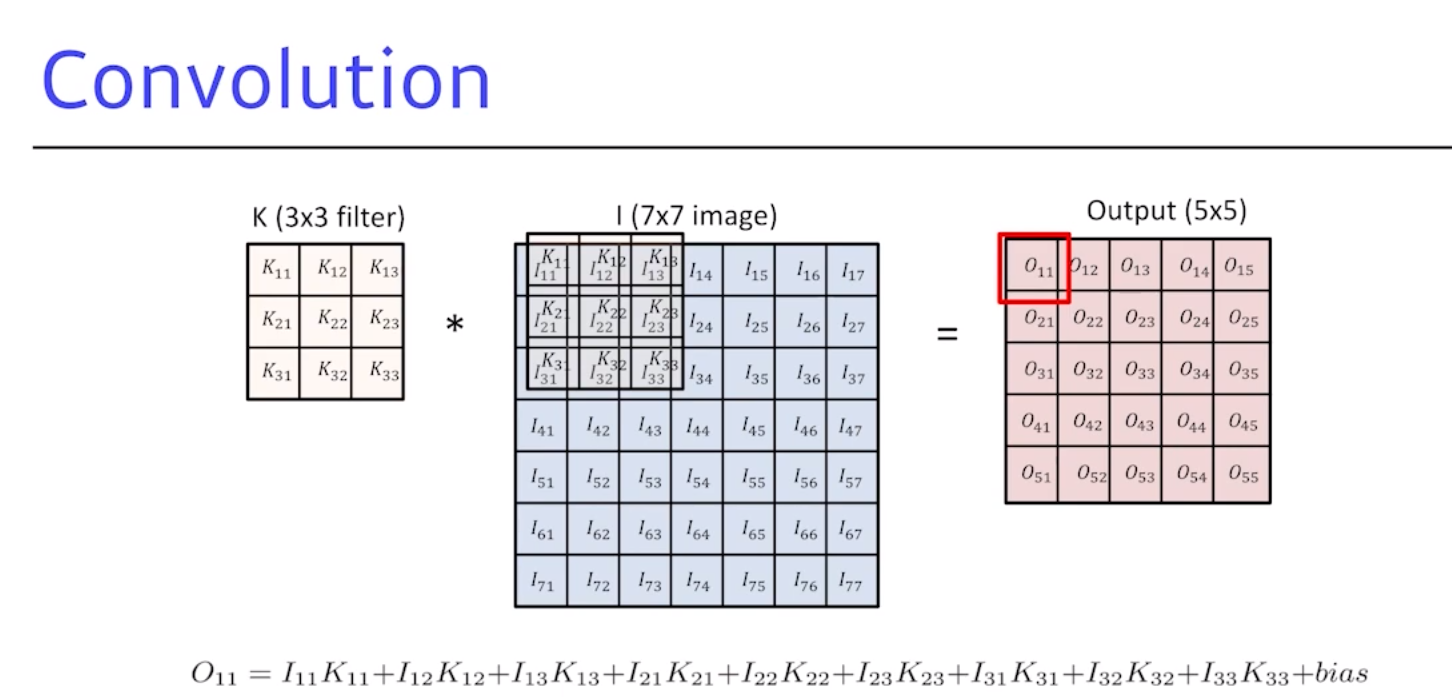
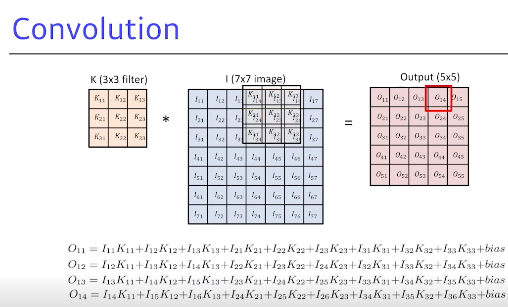
  • padding을 고려하지 않고 가장 기본적 convolution을 하면 이미지와 같이 3 by 3 필터를 7 by 7 이미지에 convolution을 하면 5 by 5 아웃풋이 나옴
  • 하나의 아웃풋 값은 convolution 필터를 적용하고자 하는 이미지에 도장을 찍는다고 보면 됨
  • 해당 위치에 있는 convolution 필터 값과 이미지의 픽셀 값을 곱해서 전체 3 by 3 필터를 더해주면 convolution Operator 혹은 2D convolution를 할 수 있음

💡 convolution operation (합성곱 연산)을 한다는 것은 어떤 의미일까?

  • 2D convolution : 해당 convolution 필터의 모양을 해당 이미지에 찍는 것으로, 적용하고자 하는 필터의 모양에 따라 같은 이미지에 대해서 그 convolution 아웃풋이 블러 또는 임보스, 아웃라인 등이 될 수 있음
    • 예를 들어 3 by 3을 쓰고 각각 필터가 9/1이 들어가 있다고 하면 3 by 3 이미지의 값의 평균이 다음 번 convolution 필터의 아웃풋이 됨
    • 그래서 이미지가 특정 영역 만큼의 픽셀값들을 다 합쳐 평균을 내기 때문에 마치 블러 효과가 일어나며, 다른 필터 모양도 강조하거나 외곽선 형태를 따는 것도 얻을 수 있음

2. RGB Image Convolution

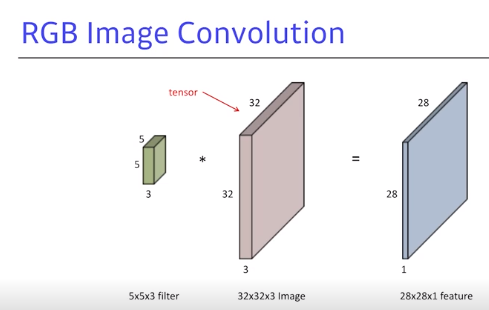
  • 일반적으로 다루는 것은 RGB 이미지
  • tensor로 표현하며 32 by 32 by 3짜리 이미지 depth 방향으로 3 by 채널 RGB가 들어가게 됨
  • 32 by 32 by 3짜리 이미지를 convolution한다고 하면 5 by convolution을 한다고 해도 필터의 값이 항상 같다는 건 숨겨져 있음
  • 그래서 5 by 5 필터를 한다는 것은 5 by 5 by 3짜리 convolution 필터를 사용한다는 것이며, 아웃풋은 28 by 28 by 1이 됨 (32-5+1) by (32-5+1) by (3-3+1)

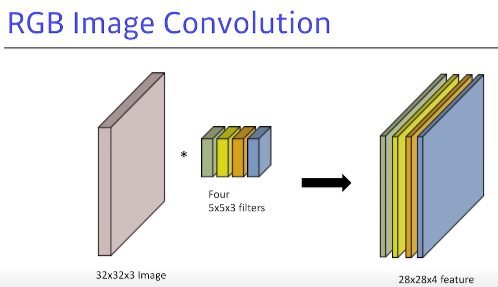
  • 일반적으로 convolution을 생각하면 이미지가 들어가서 여러 개의 채널을 밭는 convolution 피쳐 맵이 나오게 됨
  • 이 피쳐 맵의 채널 숫자가 생기는 것은 convolution 필터가 여러 개 있다고 볼 수 있음
  • 32 by 32 by 3에 5 by 5 by 3 필터를 적용하면 그 아웃풋의 채널은 1이 됨
    • 이 때, 만약 그러한 convolution필터가 4개가 있다면? → 4개에 맞춰 아웃풋 역시 28 by 28 by 4가 됨
  • 인풋 채널과 아웃풋 convolution 피쳐맵의 채널을 알면 여기에 적용되는 convolution 피쳐에 크기 역시 같이 계산 가능

3. Stack of Convolutions

  • Stack of convolution : Conv를 여러 번 할 수 있음
  • 32 by 32 by 3 이미지가 들어가 5 by Conv을 했는데, 그 다음 피쳐맵이 4 채널이 나오려면 4개의 5 by 5 by 3 필터가 필요
  • 그리고, 그렇게 나온 Conv 피처맵에 각 요소별로 Activation function, nonlinier activation을 통과시키게 됨
  • ReLU는 요소별로 0보다 작은 값은 0으로 바꾸고, 0보다 큰 값은 그대로 씀
    • 조심해야할 것은 이 연산에 필요한 파라미터의 숫자를 잘 생각해야 함
  • 32 by 32 by 3짜리 RGB 이미지를 28 by 28 by 4짜리 convolution feature를 얻기 위해 필요한 파라미터의 수는 5 by 5 by 3 by 4가 됨
  • 커널의 사이즈에서 인풋 채널 숫자만큼이 파라미터 수가 됨
  • 다음 번 피쳐맵이 24 by 24 by 10이면, 10개의 Conv 필터가 필요하고, 각각 Conv 필터 사이즈는 5 by 5 by 4가 됨, 4는 Conv하는 feature의 디멘젼이 됨

4. Convolutional Neural Networks

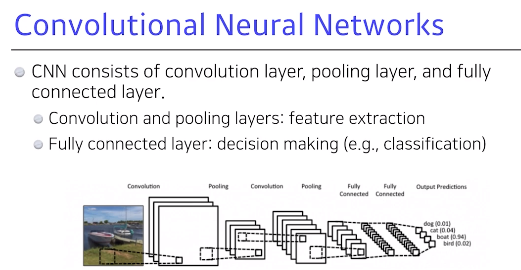
  • pooling layer : 마지막에 모두 합쳐 최종적으로 원하는 결과값을 만들어주는 Fully connected layer가 됨
  • convolution과 pooling layer가 할 수 있는 것은 이미지에서 유용한 정보를 뽑아주는 feature extraction
  • Fully connected layer : decision making 분류, 폐기해서 원하는 출력값을 얻어줌
  • 이렇게 만들어지는 게 일반적이나, 최근 Fully connected layer를 최소화 함
  • 이유는 파라미터 숫자의 dependent를 하게 되는데, 우리가 머신러닝에서 일반적으로 알려진 것은 학습하거나 어떤 모델의 파라미터의 숫자가 늘어날수록 학습이 어렵고, 또 generation 퍼포먼스가 떨어진다고 알려져 있음
  • 아무리 학습을 잘 시켜도 실생활 나가서 이 모델을 적용하먼 성능이 잘 안나옴
  • CNN이 발전하는 방향은 같은 모델을 만들고 최대한 모델을 deep하게 많이 가져가지만, 동시에 파라미터 숫자를 줄이는데 집중하게 됨
  • 이를 위한 테크닉을 앞으로 배우게 될 것
  • 강조하는 것은 NN를 봤을 때, 이 네트워크의 레이어 별로 몇 개의 파라미터로 이루어져 있고 전체 파라미터가 몇 개인지 감을 갖고 있는 것이 중요

5. Convolution Arithmetic (of GoogLeNet)

  • GoogLeNet에 있는 표
    • 어떤 NN에 대해 파라미터가 몇 개인지, 이 표가 정말 맞는지 계산해 보는 것이 좋음

6. Stride

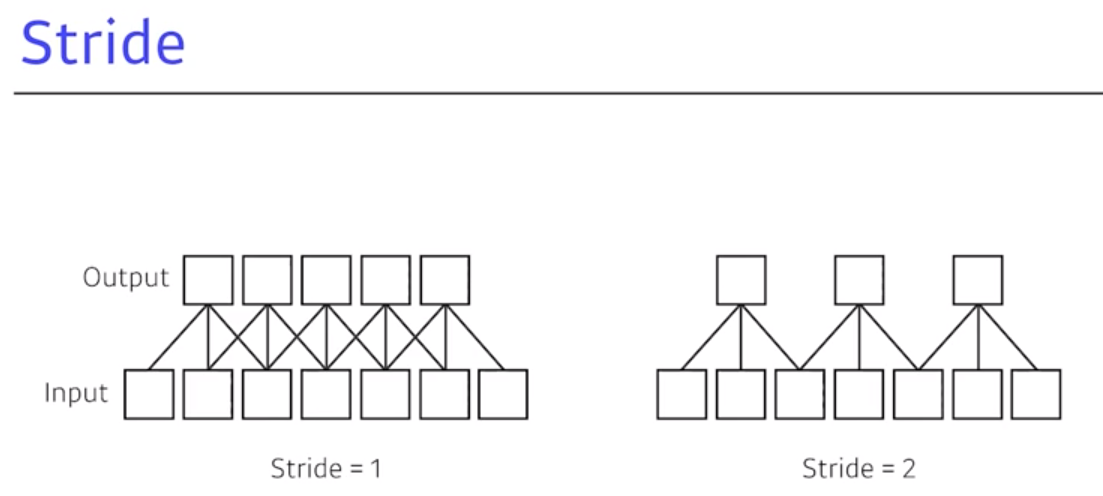
  • stride : 넓게 걷는다라는 의미로 3 by 3, 5 by 5는 모든 Stride가 1, 커널을 매 픽셀마다 1씩 찍고 다음 픽셀마다 1씩 찍음
  • 1D를 그린다고 가정하고 7개의 인풋, 3의 커널이 있을 때, 아웃풋을 만들면 Stride=1인 경우 첫 번째 그림처럼 5개의 아웃풋이 나옴
  • Stride가 2개일 때 똑같이 7개 인풋, 3짜리 커널이 있을 때, 필터 하나 찍고 바로 옆으로 가는 것이 아닌 2칸을 옮김
  • 1 by 1 stride, 1 by 2 or 2 by 2 stride … 이런 식의 stride처럼 씀

7. Padding

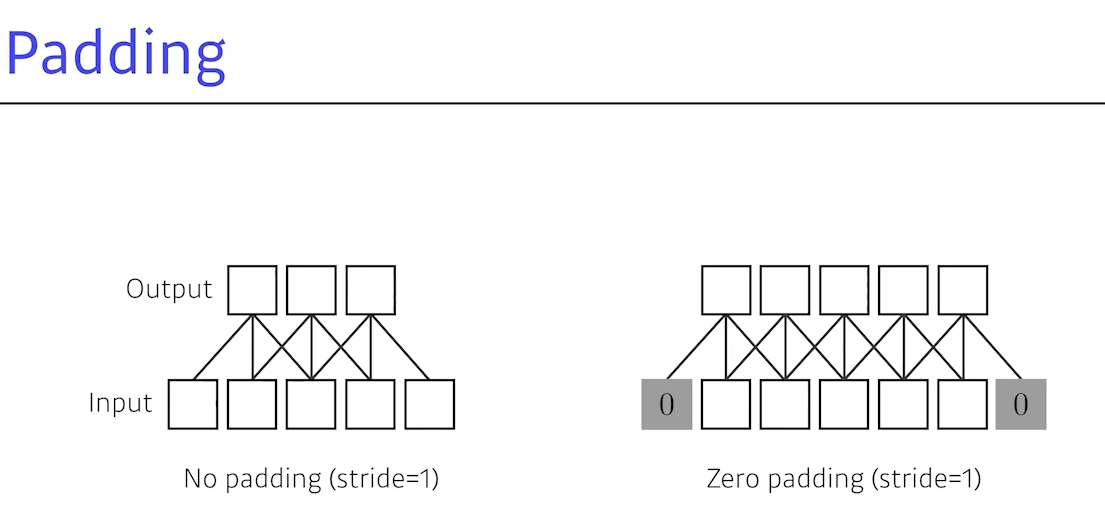
  • Padding : 어떤 인풋이 있을 때 convolution operation을 하면 똑같이 안 나오는데, 그 이유는 바운더의 정보가 버려지기 때문
  • Padding : 어떤 값을 덧대주는 것, zero padding : 덧대주는 값이 0이 되는 것
  • 즉 5개의 입력이 있을 때 3 by 3 by 3의 convolution이 있으면 아웃풋이 3개가 됨
  • 그러나 2번째 이미지처럼 제곱 padding을 하고 stride를 1을 하면, 인풋과 아웃풋의 space dimension이 똑같게 됨

8. Stride? Padding?

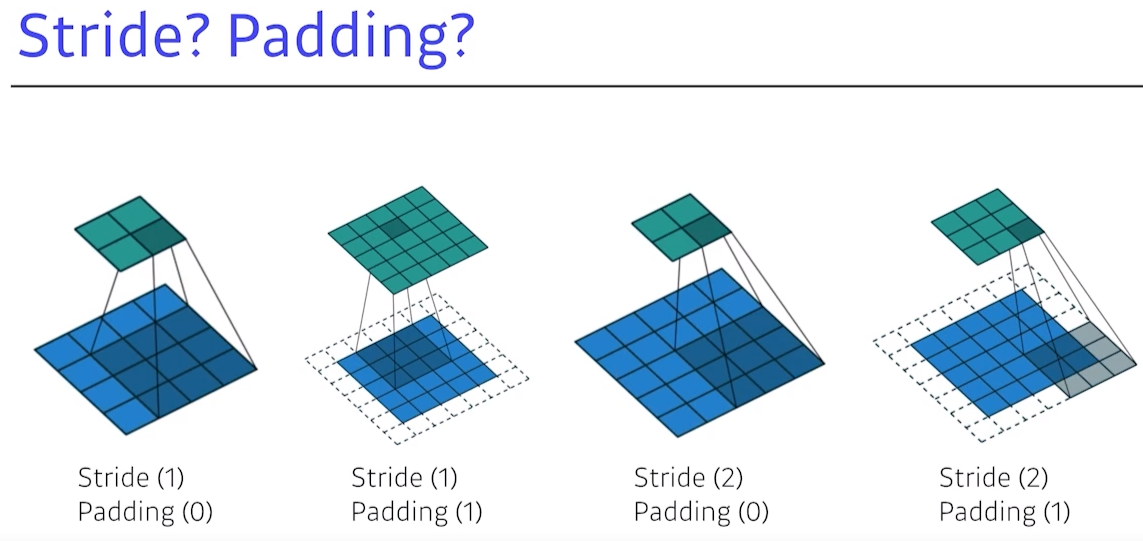
  • 첫 번째 : 3 by 3 Conv가 이뤄지고 있고, 이경우 stride=1, padding=0
    • 그 이유는 1칸씩 옮기며 아웃풋을 옮기고 zero padding이 없기 때문
  • 두 번째 : Conv 필터를 1칸씩 움직여서 stride=1, padding=1
    • Conv 필터가 주어졌을 때 적절한 크기의 zero padding 혹은 padding이 들어가 있고 stride = 1이면, 입력과 그 convolution operation의 출력인 Conv 피쳐맵의 디멘젼이 같아지는 것을 알 수 있음
    • 물론 3 by 3 필터를 하기 때문에 padding=1이 되지만, 만약 5 by 5의 경우 padding=2가 필요하고, 7 by 7이면 padding=3이 필요할 것
      • 즉, 적절한 크기의 padding을 하고 stride=1이면 항상 같은 결과가 나옴
  • 세 번째 : Conv 필터가 1칸 건너 감, stride=2, padding=0
  • 네 번째 : padding이 있어 가장자리를 찍을 수 있고, 2칸에 걸쳐 operation이 되기 때문에 stride=2, padding=1
  • 이와같이 인풋이 있고 Conv 피쳐맵이 있으며 convolution operation을 할 때, 원하는 출력 값에 맞춰 stride를 줘서 연관을 지을 수 있음

9. Convolution Arithmetic

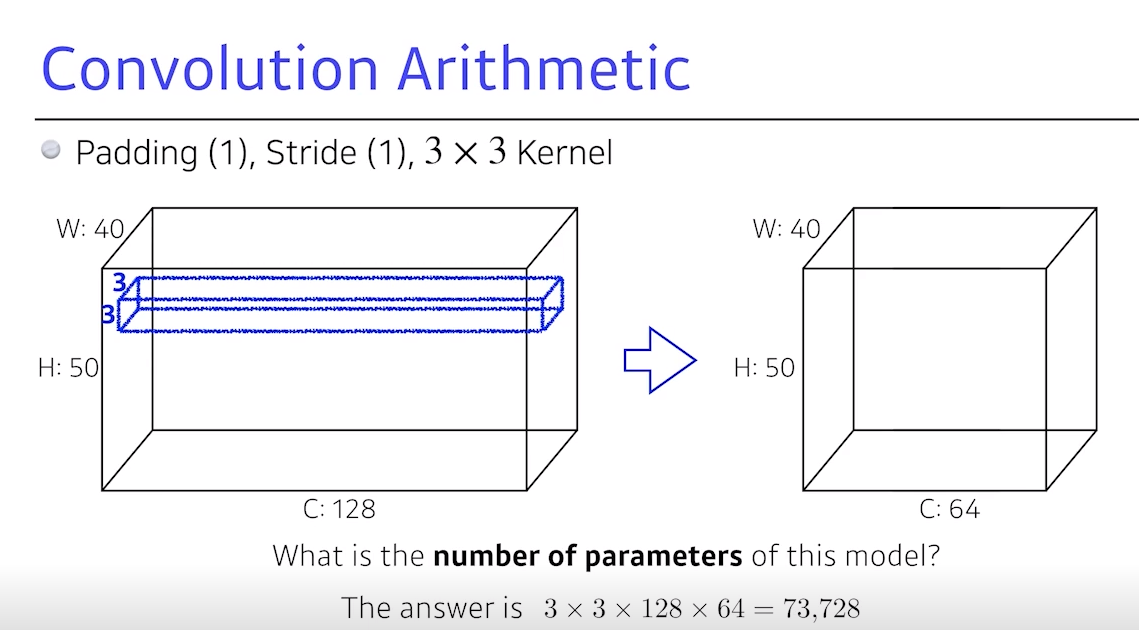
  • 파라미터 숫자 계산
  • W와 H의 space dimension에 40 by 50 입력이 있고 C=128 출력에, 40 by 50, 채널=64, 3 by 3 커널을 사용하는 조건이 주어져 있음

Q. 이 Conv 레이어를 정의하기 위한 파라미터가 몇 개일까?

  • Conv 피쳐맵, Conv operation으로 나오는 한 채널을 만들기 위해, 기본적으로 Conv하고 싶은 커널의 space dimension이 있어야 하고, 자동으로 숨겨져 있지만, 각각 커널의 채널 크기는 인풋 디멘젼과 똑같게 됨
  • 그래서 하나의 Conv 피쳐, 필터, 혹은 커널의 크기는 3 by 3 by 128
  • 이처럼 3 by 3 by 128을 찍고 stride=1, padding=1이 되면, 40 by 50 by space dimension에 채널 1개가 나옴
  • 그러나 궁극적으로 채널 64개를 원하므로, 결국 Conv 필터가 64개 필요함 → 3 x 3 x 128 x 64 = 76,728개
  • padding, stride는 파라미터 숫자와 무관하며, 파라미터의 숫자는 오로지 커널, 필터가 몇 개 있는지가 중요할 것임
  • 이에 대한 계산이 자동으로 돼야 하며, 각각 네트워크 파라미터의 모양만 봐도 단위 개념으로 감이 생겨야 할 것

10. Exercise

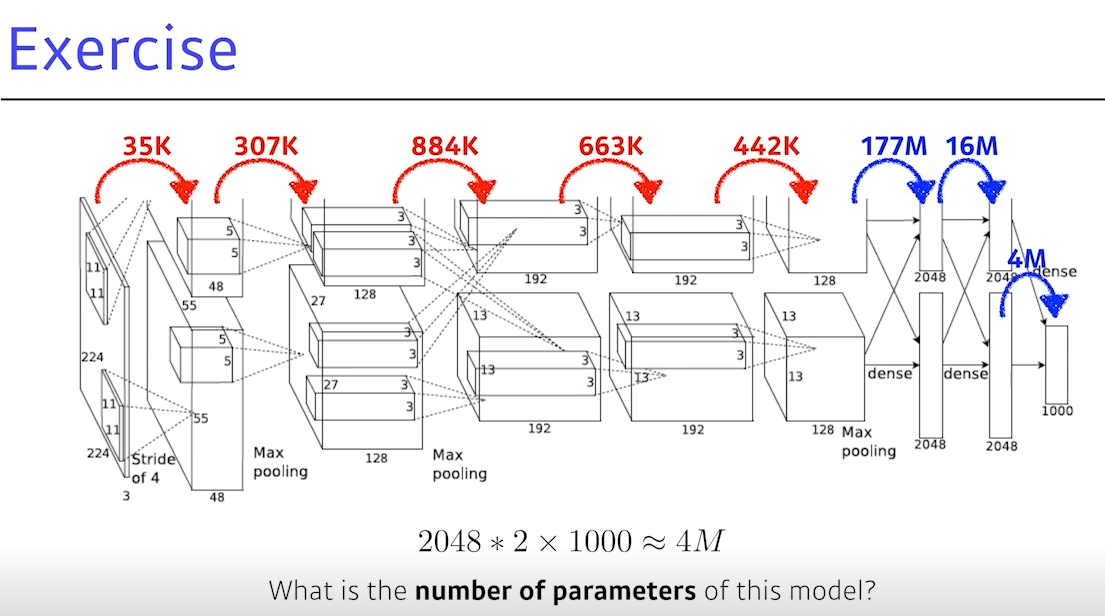
(알렉스넷 모델이며, 지금의 딥러닝의 위상을 갖게한 것)

  • 첫번째 레이어에서 알수 있는 건 입력으로 들어온 이미지가 224 by 224 by 3인 것으로, 11 by 11 Conv이 이뤄짐 숨겨진 것은 각각 1개의 커널(필터)는 11 by 11 by 3이겠구나라는 것
  • 다음 레이어를 보면 알렉스넷은 네트워크가 2개의 패스로 갈라지는데 그 이유는 그 때 당시 gpu 메모리가 크지 않아 2개로 나눴던 것 (중요 x)
  • layer 1 : 11 x 11 x 3 x 48 * 2 = 35k → *2는 gpu 이슈 때문
  • layer 2 : 5 by 5로 필터의 크기가 줄어듦, 5 x 5 x 48 x 128 * 2 = 307k
  • layer 3 : 3 by 3으로 필터가 줄었지만, 인풋, 아웃풋의 채널이 엄청 커짐 3 x 3 x 128 * 2 x 192 * 2 = 884k
  • layer 4 : 3 x 3 x 192 x 192 * 2 = 663k (약간 줄어듦)
  • layer 5 : 3 x 3 x 192 x 128 * 2 = 442k
  • layer 6 : 13 x 13 x 128 *2 x 2048 *2 = 177M
  • layer 7 : 2048 * 2 x 2048 * 2 = 16M
  • layer 8 : 2048 * 2 x 1000 = 4M
  • 중요한 것은 여기서 본 파라미터 숫자는 대부분 커봤자 884K정도
  • 여기서부터는 dense layer로 이 차원은 인풋 뉴럴의 개수와 아웃풋 뉴럴의 개수를 곱한 것으로 쉽게 생각하면 13 x 13이 채널의 값, 128이 채널숫자, & x2 , 마지막으로 출력값이 2048x2가 있으니 값이 엄청 커짐
  • 그래서 빨간색 레이어가 Conv layer 이고, 파란색은 dense layer
  • 파라미터의 숫자가 dense layer로 넘어가며 거의 1000배가 늘어나게 되는데, 그 이유는 네트워크가 인풋에서 아웃풋으로 넘어갈 때 크기가 크게 변경되는게 아님에도, dense layer가 일반적으로 많은 파라미터를 갖는 이유는 Conv operator의 각각 하나의 커널이 모든 위치에 대해 동일하게 적용되기 때문
  • NN의 성능을 올리기 위해 파라미터를 줄이는 것이 중요하고, 네트워크가 발전되는 성향으로 봤을 때, 뒷단을 최대한 줄이고 앞단을 깊게 쌓는 것이 일반적인 트렌드
  • 그런 시도들이 1 by 1 convolution이며, NN의 깊이는 점점 깊어지지만 파라미터는 점점 줄어들게 됨

11. 1x1 Convolution

  • 이미지에서 어떤 영역을 보지 않고, 1 by 1 자체가 이미지에서 한 픽셀만 보고 채널 방향으로 줄이는 것
  • 이를 시도하는 이유는 dimension은 채널을 의미하는데 이를 128에서 32로 줄임
  • 그래서, Conv layer를 더 깊게 쌓아 파라미터를 줄일 수 있게 됨
  • 실제 1 by 1 convolution을 이용한 테크닉은 굉장히 많이 사용되므로, 꼭 알아야 함!



소통은 제가 공부하고 공유하는 원동력이 됩니다.
해당 글이 도움이 되셨다면 소중한 격려와 응원 부탁드립니다 ☺️

© 2023 Daisy. All rights reserved.